【人工智能学习之图像操作（三）】

图像滤波
- 滤波概念
- 卷积
- 平滑算子
- - 均值滤波
  - 高斯滤波
  - 中值滤波
  - 双边滤波
  - 锐化算子
  - USM锐化
  - 梯度算子
傅里叶变换
直方图
- 直方图
- 直方图均衡化
- 自适应均衡化
- 2D 直方图
- 直方图反向投影

图像滤波

滤波概念

滤波过程就是把不需要的信号频率去掉的过程
滤波操作一般用卷积操作来实现，卷积核一般称为滤波器
滤波分：低通滤波，高通滤波，中通滤波，阻带滤波
低通滤波也叫平滑滤波，可以使图像变模糊，主要用于去噪
高通滤波一般用于获取图像边缘、轮廓或梯度
中通滤波一般用于获取已知频率范围内的信号
阻带滤波一般用于去掉已知频率范围内的信号
滤波分析一般有时域分析和频域分析
时域分析是直接对信号本身进行分析
频域分析师对型号的变化快慢进行分析

卷积

import cv2
import numpy as np
src = cv2.imread(r"1.jpg")
kernel = np.array([[1, 1, 0], [1, 0, -1], [0, -1, -1]], np.float32) # 定义一个核
dst = cv2.filter2D(src, -1, kernel=kernel)
cv2.imshow("src show", src)
cv2.imshow("dst show", dst)
cv2.waitKey(0)

平滑算子

均值滤波

import cv2
src = cv2.imread(r"1.jpg")
dst = cv2.blur(src, (5,5))
cv2.imshow("src show", src)
cv2.imshow("dst show", dst)
cv2.waitKey(0)

高斯滤波

import cv2
src = cv2.imread(r"1.jpg")
dst = cv2.GaussianBlur(src, (5, 5), 0)
cv2.imshow("src show", src)
cv2.imshow("dst show", dst)
cv2.waitKey(0)

中值滤波

import cv2
src = cv2.imread(r"1.jpg")
dst = cv2.medianBlur(src, 5)
cv2.imshow("src show", src)
cv2.imshow("dst show", dst)
cv2.waitKey(0)

双边滤波

import cv2
src = cv2.imread(r"1.jpg")
dst = cv2.bilateralFilter(src,9,75,75)
cv2.imshow("src show", src)
cv2.imshow("dst show", dst)
cv2.waitKey(0)

锐化算子

Laplacian锐化

import cv2
src = cv2.imread(r"1.jpg")
kernel = np.array([[0, -1, 0], [-1, 5, -1], [0, -1, 0]], np.float32) #定义一个核
dst = cv2.filter2D(src, -1, kernel=kernel)
cv2.imshow("src show", src)
cv2.imshow("dst show", dst)
cv2.waitKey(0)

USM锐化

import cv2
src = cv2.imread(r"1.jpg")
dst = cv2.GaussianBlur(src, (5, 5), 0)
dst = cv2.addWeighted(src, 2, dst, -1, 0)
cv2.imshow("src show", src)
cv2.imshow("dst show", dst)
cv2.waitKey(0)

梯度算子

Sobel，Scharr 和 Laplacian梯度滤波器
Sobel，Scharr 其实就是求一阶或二阶导数。Scharr 是对 Sobel（使用小的卷积核求解求解梯度角度时）的优化。Laplacian 是求二阶导数
Sobel 算子是高斯平滑与微分操作的结合体，所以它的抗噪声能力很好
Scharr 滤波器是对Sobel滤波器的改进版本
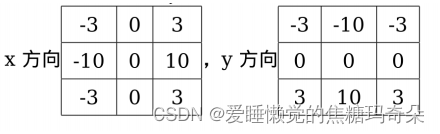
Soble算子
Scharr算子
计算梯度幅值和方向
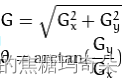
为了加快计算，用该公式简化计算
拉普拉斯算子可以使用二阶导数的形式定义，可假设其离散实现类似于二阶 Sobel 导数，事实
上，OpenCV 在计算拉普拉斯算子时直接调用 Sobel 算子
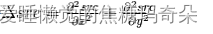
Laplacian 算子

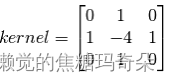
import cv2
from matplotlib import pyplot as plt
img = cv2.imread('6.jpg', 0)
laplacian = cv2.Laplacian(img, cv2.CV_64F)
sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5)
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5)
plt.subplot(2, 2, 1), plt.imshow(img, cmap='gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 2), plt.imshow(laplacian, cmap='gray')
plt.title('Laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 3), plt.imshow(sobelx, cmap='gray')
plt.title('Sobel X'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 4), plt.imshow(sobely, cmap='gray')
plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])
plt.show()

傅里叶变换

傅里叶变换原理
傅里叶变换是一种数学工具，它能够将一个复杂数学函数（或信号）从时域（即随时间变化的表现形式）转换到频域（即由不同频率的成分组成的表示形式）。它的基本思想基于这样的事实：任何连续且满足一定条件的周期信号或非周期信号都可以被分解为一系列正弦波和余弦波的无限级数或积分，这些正弦波和余弦波具有不同的频率、振幅和相位。

具体来说，如果有一个时域信号 𝑓(𝑡)，其傅里叶变换 𝐹(𝜔) 可以通过下式计算得到：
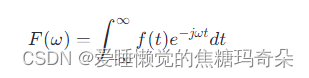
在这里插入图片描述
这里，𝜔 是频率变量，𝑒−𝑗𝜔𝑡 是复指数函数，代表不同频率的正弦波和余弦波的基础，而 𝐹(𝜔)
描述了信号在各个频率下的贡献（幅度和相位）。
原理:

使用 OpenCV 对图像进行傅里叶变换
使用 Numpy 中 FFT（快速傅里叶变换）函数

import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('1.jpg', 0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20 * np.log(np.abs(fshift))
plt.figure(figsize=(10, 10))
plt.subplot(221), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(222), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
rows, cols = img.shape
crow, ccol = rows // 2, cols // 2
fshift[crow - 30:crow + 30, ccol - 30:ccol + 30] = 0
f_ishift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.abs(img_back)
plt.subplot(223), plt.imshow(img_back, cmap='gray')
plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
plt.subplot(224), plt.imshow(img_back)
plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.show()

import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('1.jpg', 0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20 * np.log(np.abs(fshift))
plt.figure(figsize=(10, 10))
plt.subplot(221), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(222), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
rows, cols = img.shape
crow, ccol = rows // 2, cols // 2
fshift[crow - 30:crow + 30, ccol - 30:ccol + 30] = 0
f_ishift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.abs(img_back)
plt.subplot(223), plt.imshow(img_back, cmap='gray')
plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
plt.subplot(224), plt.imshow(img_back)
plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.show()

直方图

import cv2
import matplotlib.pyplot as plt
img = cv2.imread('1.jpg')
img_B = cv2.calcHist([img], [0], None, [256], [0, 256])
plt.plot(img_B, label='B', color='b')
img_G = cv2.calcHist([img], [1], None, [256], [0, 256])
plt.plot(img_G, label='G', color='g')
img_R = cv2.calcHist([img], [2], None, [256], [0, 256])
plt.plot(img_R, label='R', color='r')
plt.show()

直方图均衡化

import cv2
import matplotlib.pyplot as plt
img = cv2.imread('2.jpg', 0)
cv2.imshow("src", img)
his = cv2.calcHist([img], [0], None, [256], [0, 256])
plt.plot(his, label='his', color='r')
# plt.show()
dst = cv2.equalizeHist(img)
cv2.imshow("dst", dst)
cv2.imwrite("15.jpg", dst)
his = cv2.calcHist([dst], [0], None, [256], [0, 256])
plt.plot(his, label='his', color='b')
plt.show()

自适应均衡化

自适应直方图均衡化是对图片的每一个局部进行均衡化操作

import cv2
img = cv2.imread('3.jpg', 0)
cv2.imshow("src", img)
dst1 = cv2.equalizeHist(img)
cv2.imshow("dst1", dst1)
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8))
dst2 = clahe.apply(img)
cv2.imshow("dst2", dst2)
cv2.waitKey(0)

2D 直方图

在前面的部分我们介绍了如何绘制一维直方图，之所以称为一维，是因为我们只考虑了图像的一个
特征：灰度值。但是在 2D 直方图中我们就要考虑两个图像特征。对于彩色图像的直方图通常情况
下我们需要考虑每个的颜色（Hue）和饱和度（Saturation）。根据这两个特征绘制 2D 直方图。

import cv2
img = cv2.imread('3.jpg')
hsv = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)
hist = cv2.calcHist([hsv], [0, 1], None, [180, 256], [0, 180, 0, 256])
cv2.imshow("hist",hist)
cv2.waitKey(0)

直方图反向投影

它可以用来做图像分割，或者在图像中找寻我们感兴趣的部分。简单来说，它会输出与输入图像（待搜索）同样大小的图像，其中的每一个像素值代表了输入图像上对应点属于目标对象的概率。用更简单的话来解释，输出图像中像素值越高（越白）的点就越可能代表我们要搜索的目标（在输入图像所在的位置）。这是一个直观的解释。直方图投影经常与 camshift算法等一起使用。
我们要查找的对象要尽量占满这张图像（换句话说，这张图像上最好是有且仅有我们要查找的对象）。最好使用颜色直方图，因为一个物体的颜色要比它的灰度能更好的被用来进行图像分割与对象识别。接着我们再把这个颜色直方图投影到输入图像中寻找我们的目标，也就是找到输入图像中的每一个像素点的像素值在直方图中对应的概率，这样我们就得到一个概率图像，最后设置适当的阈值对概率图像进行二值化。

import cv2
import numpy as np
roi = cv2.imread('7.jpg')
hsv = cv2.cvtColor(roi,cv2.COLOR_BGR2HSV)
target = cv2.imread('6.jpg')
hsvt = cv2.cvtColor(target,cv2.COLOR_BGR2HSV)
roihist = cv2.calcHist([hsv],[0, 1], None, [180, 256], [0, 180, 0, 256] )
cv2.normalize(roihist,roihist,0,255,cv2.NORM_MINMAX)
dst = cv2.calcBackProject([hsvt],[0,1],roihist,[0,180,0,256],1)
disc = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(5,5))
dst=cv2.filter2D(dst,-1,disc)
ret,thresh = cv2.threshold(dst,50,255,0)
thresh = cv2.merge((thresh,thresh,thresh))
res = cv2.bitwise_and(target,thresh)
res = np.hstack((target,thresh,res))
cv2.imwrite('65.jpg',res)
cv2.imshow('img',res)
cv2.waitKey(0)